Efficient Quantum Machine Learning with a Modified Depolarization Approach

As the quantum computing community navigates the NISQ (Noisy Intermediate-Scale Quantum) era, managing noise poses a prominent challenge, particularly in Quantum Machine Learning (QML). Quantum systems inherently exhibit noise, which can drastically impact computational accuracy. Notably, depolarization noise, a prevalent noise model in quantum computing, presents a formidable obstacle in developing efficient QML models. The paper “A Modified Depolarization Approach for Efficient Quantum Machine Learning” introduces a modified representation of the depolarization channel for a single-qubit. The proposed modified channel uses two Kraus operators based only on X and Z Pauli matrices. The approach reduces the computational complexity from six to four matrix multiplications per channel execution.

What’s Depolarization, and Why Does It Matter?

Depolarization is a noise process where a quantum state collapses, with some probability, into a mixed state, essentially scrambling the information. For example, imagine working with a quantum bit (qubit) represented by a density matrix $\rho$ . In the traditional depolarization model, noise can be introduced by applying the three Pauli matrices — X, Y, and Z to $\rho$ with equal probability. Mathematically, this looks like:

(1) $\begin{equation*} \rho \rightarrow (1 - p) \rho + \frac{p}{3} (X \rho X + Y \rho Y + Z \rho Z)\end{equation*}$

where $p$ is the probability of depolarization. Each of the Pauli operators represents a potential disturbance to the qubit. The more noise we apply, the more the system deteriorates. However, simulating this noise is computationally expensive, especially in large quantum systems, as it requires a substantial number of matrix multiplications. This is where the paper’s novel contribution shines.

The Power of Modified Depolarization Channel and Two Kraus Operators

The central innovation of this paper is an alternative representation of the depolarization channel characterized by reduced matrix multiplication operations that only use the $X$ and $Z$ Pauli matrices.

(2) $\begin{equation*} \rho_{m}' = (1 - \frac{2p}{3}) \rho + \frac{2p}{3} Z((\rho X)^T X) Z\end{equation*}$

Traditionally, depolarization uses three Kraus operators, each corresponding to one of the Pauli matrices. In practical terms, this means that when we’re simulating a quantum system with noise, we need to perform six matrix multiplications per qubit per step—this scales rapidly with the size of the system. The modified depolarization approach in the paper proposes reducing the number of Kraus operators to two by cleverly using only the $X$ and $Z$ Pauli matrices, allowing for more efficient simulation without significantly compromising the accuracy of the noise model. The two Kraus operators are defined as:

$\begin{array}{cc}K_0 = \sqrt{1 -\frac{2p}{3}} \mathbb{I}, &K_1 = i \sqrt{\frac{2p}{3}} ZX .\end{array}$

The author provides meticulous proof to assert the proposed modified expression’s authenticity and Kraus operators’ authenticity. This seemingly small change reduces the number of required matrix multiplications from six to four, a non-trivial improvement in computational cost. This reduction becomes especially significant as quantum circuits grow deeper and larger—common in QML algorithms, where we often have to run complex iterative procedures.

Experimenting with Quantum Machine Learning on the Iris Dataset

To validate their approach, the authors experimented with a well-known machine learning problem: classifying the Iris dataset using the Iris dataset by training a variational quantum circuit under a modified depolarization noise channel. Their results verify that the modified depolarization channel accurately represents channel evolution for different values of $p$ , and these results are consistent with simulation results. Once the Iris dataset was encoded into quantum states, the author trained the QML model under noisy conditions using the modified depolarization method. Thanks to Pennylane Library, the authors claim to implement the modified channel efficiently. The findings were fascinating: the computational load was reduced by 1.5 to 2 times compared to the traditional depolarization method, while classification accuracy remained comparable. This is a big deal for QML. Efficiency in quantum simulations is crucial—especially given the already limited coherence times and high noise levels of NISQ devices. Reducing computational cost allows for quicker experimentation and larger models, accelerating the development of quantum machine learning algorithms. The following figure provides the decision boundaries for readers’ reference. We request that the readers to refer to the original manuscript for in-depth analysis.

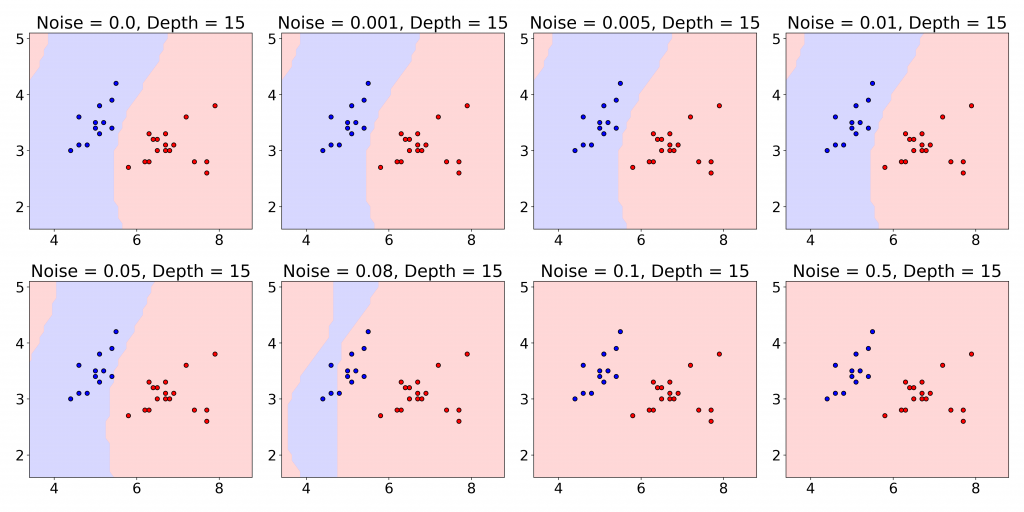
An increase in circuit depth may enhance the model’s expressivity, but it also increases its vulnerability to noise, which adversely affects the quality of the decision boundary.

Why This Matters for the NISQ Era

We’re still far from having fault-tolerant quantum computers (except google’s latest work) that can operate indefinitely without errors. For now, we must work with what we’ve got: noisy, small to mid-scale quantum devices. This means any improvement in the efficiency of noise simulation or error mitigation has a direct and significant impact on the feasibility of using quantum systems for practical problems.

The reduction in computational overhead offered by this modified depolarization approach is particularly relevant for QML, where deep quantum circuits and iterative optimization processes require substantial computational resources. This is a step toward making QML more scalable and closer to real-world applications, even within the limitations of today’s quantum technology.

Looking Ahead

As quantum hardware continues to evolve, so too will the need for more efficient noise models and error mitigation techniques. The modified depolarization approach presented in this paper offers a glimpse into how we can make QML more computationally feasible. While the improvement in noise simulation efficiency may seem small, these incremental advancements will enable the quantum systems of the future to handle more complex and meaningful tasks.

I’m excited to see how this approach will be applied to larger quantum systems and more complex QML models. The road to fully realizing quantum machine learning’s potential is long, but innovations like this bring us one step closer.

For a detailed exploration of the methodology and findings, read the full paper at: https://www.mdpi.com/2227-7390/12/9/1385

References

Khanal, Bikram, and Pablo Rivas. “A Modified Depolarization Approach for Efficient Quantum Machine Learning.” Mathematics 12.9 (2024): 1385.

About the Author

Bikram Khanal is a Ph.D. student at Baylor University, specializing in Quantum Machine Learning and Natural Language Processing.