In the rapidly evolving field of Quantum Machine Learning (QML), one of the most pressing challenges is handling noise—the errors that naturally arise in quantum systems, particularly in the Noisy Intermediate-Scale Quantum (NISQ) era. But what if we could teach quantum systems to “learn” and address noise head-on? Our paper “Learning Robust Observable to Address Noise in Quantum Machine Learning” explores an approach to mitigating this issue by focusing on learning robust observables. These observables can withstand the effects of noise, improving the performance of QML models in noisy environments.
Understanding the Problem of Noise in QML
In quantum systems, noise comes from imperfections in quantum gates, interactions with the environment, and decoherence—making quantum computations highly error-prone. When applying QML, this noise leads to inaccuracies in predictions and model training. This research aims to identify observables that remain invariant or change minimally even in the presence of noise, thus offering more reliable outputs from quantum systems.
The Framework: Learning Robust Observables
We propose a machine learning-based framework to find observables that are inherently resistant to various types of noise. To tackle this, we propose training a machine learning model to identify observables that remain invariant or less susceptible to noise. The model learns from the behavior of quantum states passing through noisy channels and adjusts to find robust observables that maintain their integrity despite noise. We illustrate the problem using a Bell state (a well-known quantum state), subjecting it to a depolarization channel to simulate noise.
The process can be formalized as an optimization problem where the goal is to minimize the change in the expectation value of the observable when the quantum state is subject to noise. Mathematically, this can be expressed as minimizing:
![]()
Here, ![]() is a Pauli-Z observable, and
is a Pauli-Z observable, and ![]() is an observable we are trying to learn. The expectation value is computed before and after noise is introduced. The goal is to find an observable that minimizes this difference, effectively learning a robust observable.
is an observable we are trying to learn. The expectation value is computed before and after noise is introduced. The goal is to find an observable that minimizes this difference, effectively learning a robust observable.
A Toy Example
In our framework, we train QML models by simulating quantum systems across different noise channels, including depolarization, amplitude damping, phase damping, bit flip, and phase flip channels. The objective is to learn observables for various quantum circuits—such as Bell state circuits, Quantum Fourier Transform circuits, and highly entangled random circuits—that can remain robust across different noise levels. The framework demonstrated that it could identify an observable that better retains the state’s properties under noisy conditions, proving that robust observables can be learned effectively.
Consider the following example:
(1) 
We computed its expectation value for Bell’s states under varying degrees of depolarization, ![]() . The expectation values of the observable
. The expectation values of the observable ![]() on the depolarized Bell state as a function of the depolarization rate
on the depolarized Bell state as a function of the depolarization rate ![]() are plotted in the following figure.
are plotted in the following figure.
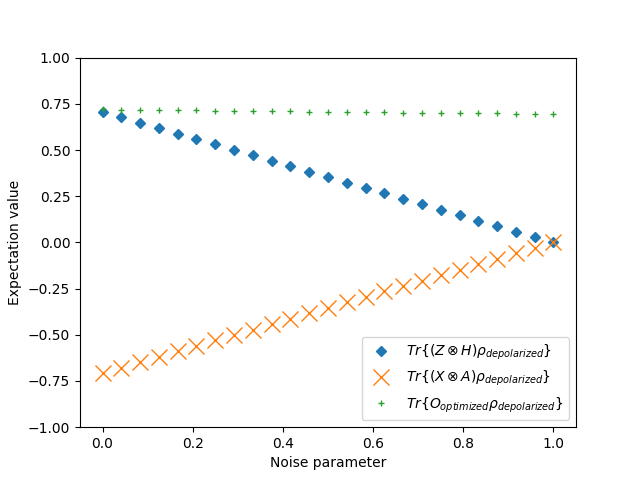
In this figure, ![]() is the Pauli-Z matrix,
is the Pauli-Z matrix, ![]() is the Pauli-X matrix,
is the Pauli-X matrix, ![]() is the Hadamard gate,
is the Hadamard gate, ![]() is an arbitrary observable, and
is an arbitrary observable, and ![]() is a learned single qubit Hermitian measurement operator. This toy example shows that the expectation value of the custom observable
is a learned single qubit Hermitian measurement operator. This toy example shows that the expectation value of the custom observable ![]() on the depolarized Bell state remains constant as the depolarization rate
on the depolarized Bell state remains constant as the depolarization rate ![]() increases.
increases.
Key Findings
- Custom observables designed through this method demonstrated remarkable stability against noise, especially when compared to traditional observables like Pauli matrices.
- In noisy channels like depolarization, the learned observables maintained a more consistent expectation value, while traditional observables exhibited greater variance.
- The approach can be applied to various types of quantum circuits, making it versatile and broadly applicable in enhancing the reliability of QML models.
Implications for Quantum Machine Learning
This study offers a promising avenue for improving the accuracy and stability of QML in real-world applications. By learning robust observables, QML systems can perform more reliably, even as we contend with the inherent noise in current quantum computers. By using learned observables, the performance of quantum machine learning models can be made more stable, even when operating in the inherently noisy NISQ regime. This has implications for advancing practical applications of quantum computing, especially as we seek to scale up quantum algorithms in the near-term.
Looking Ahead: The Future of Noise-Resistant QML
The results from this paper open up exciting possibilities for future work. Imagine a future where every quantum machine learning algorithm can autonomously adjust to different noisy environments by learning which observables to trust. This would make QML models more resilient and, ultimately, more practical for real-world applications.
One immediate future direction is testing the framework on larger systems and more complex noise models. Additionally, combining this method with error correction techniques could further enhance the stability of QML algorithms.
For a detailed exploration of the methodology and findings, read the full paper at:
https://arxiv.org/pdf/2409.07632
References
- Khanal, Bikram, and Pablo Rivas. “Learning Robust Observable to Address Noise in Quantum Machine Learning.” arXiv preprint arXiv:2409.07632 (2024).
About the Author
Bikram Khanal is a Ph.D. student at Baylor University, specializing in Quantum Machine Learning and Natural Language Processing.

