Brain-Computer Interfaces and AI: Technology Overview and Current Capabilities

The emergence of brain-computer interfaces (BCIs), particularly those developed by companies like Neuralink, represents a key convergence of neuroscience and AI. These technologies aim to facilitate direct communication between the human brain and external devices, offering wide-ranging applications in healthcare, education, and even entertainment. For instance, BCIs can assist people with disabilities or potentially boost cognitive functions in the general population. When AI is added to the mix, it can interpret neural signals in real-time, resulting in more natural and fluid ways of interacting with computers (İbişağaoğlu, 2024; Silva, 2018).

What Are BCIs?

A brain-computer interface is a system that establishes a direct communication pathway between the brain and an external device. The goal is to translate brain activity into actionable outputs, such as controlling a robotic arm or a computer cursor.

BCIs operate in two main modes:

Open-loop systems: These send information from the brain to an external device but don’t provide feedback to the user. An example would be a system that controls a prosthetic hand based on neural signals without sensory feedback.
Closed-loop systems: These provide feedback to the user, creating a dynamic interaction. For instance, a robotic limb that not only moves based on brain signals but also sends sensory feedback about grip strength (Voeneky et al., 2022).

Types of BCIs: Non-Invasive, Semi-Invasive, and Invasive

There are three primary types of BCIs, differentiated by how they access neural signals:

Non-Invasive BCIs:
- These use external devices to read brain signals, typically via electroencephalography (EEG). EEG BCIs detect electrical activity from the scalp and are widely used in research and consumer applications like gaming and neurofeedback for mental health.Advantages: Low risk, no surgery required, relatively affordable.Limitations: Low signal resolution due to the skull dampening signals. This limits their use in high-precision tasks.
Example: Devices like Emotiv’s headsets, which enable basic control of devices, such as turning on a light by focusing attention (Silva, 2018).
Semi-Invasive BCIs:
- These involve placing electrodes on the surface of the brain but outside the brain tissue. This technique, known as electrocorticography (ECoG), is often used in medical settings.Advantages: Higher signal resolution compared to EEG, without penetrating brain tissue.Limitations: Requires surgery, so it’s less commonly used outside clinical or experimental settings.
Example: ECoG BCIs have been used to help people with epilepsy control devices or communicate (Kellmeyer, 2019).
Invasive BCIs:
- These are the most advanced BCIs, involving implanted electrodes directly into brain tissue. The Utah Array, for instance, offers extremely high signal resolution by recording activity from individual neurons.Advantages: High precision, allowing for fine motor control and complex tasks like operating robotic limbs or even restoring movement in paralyzed individuals.Limitations: High risk of infection, expensive, and requires surgery.
Example: Neuralink’s ongoing research demonstrates the use of implanted BCIs for controlling devices and potentially restoring vision or mobility in the future (Yuste et al., 2017).

Applications and Current Capabilities

BCI technology has practical applications in several fields:

Assistive Technologies:
- BCIs allow people with disabilities to control wheelchairs, robotic arms, or communication devices. For example, people with ALS can use BCIs to type out words via thought alone (Salles, 2024).
Rehabilitation:
- In closed-loop BCIs, neurofeedback can help stroke patients regain motor function by retraining brain circuits (Voeneky, 2022).
Neuroscience Research:
- BCIs provide tools for understanding brain function, from motor control to decision-making processes (Kellmeyer, 2019).
Consumer Applications:
- Emerging technologies are exploring non-invasive BCIs for gaming, meditation, and even controlling smart home devices (Silva, 2018).

The Future of BCIs

While BCIs hold great promise, several challenges prevent them from becoming affordable, practical tools for widespread use:

Signal Quality and Noise:
- Non-invasive BCIs like EEG face significant signal interference from the skull and scalp, reducing their accuracy and reliability. Improving hardware to capture clearer signals without invasive procedures is a major hurdle (Sivanagaraju, 2024).
Scalability and Cost:
- Invasive BCIs, such as those using the Utah Array, require complex surgical procedures and highly specialized equipment, driving up costs. Making these systems accessible at scale requires breakthroughs in manufacturing and less invasive implantation techniques (Yuste et al., 2017).
Data Processing and AI:
- Decoding brain signals into usable outputs requires advanced algorithms and computational power. While machine learning has made strides, real-time, low-latency decoding remains a technical challenge, especially for complex tasks (İbişağaoğlu, 2024).
Durability of Implants:
- For invasive systems, implanted electrodes face degradation over time due to the body’s immune response. Developing materials and designs that can endure for years without significant loss of function is essential for long-term use (Farisco et al., 2022).
User Training and Usability:
- Current BCIs often require extensive training to operate effectively, which can be a barrier for users. Simplifying interfaces and reducing the learning curve are critical for consumer adoption (Silva, 2018).

These technical hurdles must be addressed to make BCIs a reliable, affordable, and practical reality. Overcoming these challenges will require innovations in materials, signal processing, and user interface design, all while ensuring safety and scalability.

Conclusion

BCIs are no longer science fiction. They are active tools in research, rehabilitation, and assistive technologies. The distinction between open-loop and closed-loop systems, as well as the differences between non-invasive, semi-invasive, and invasive approaches, defines the current landscape of BCI development. I hope this overview provides a solid foundation for exploring the ethical and philosophical questions that follow.

References:

İbişağaoğlu, D. (2024). Neuro-responsive AI: Pioneering brain-computer interfaces for enhanced human-computer interaction. NFLSAI, 8(1), 115.
Silva, G. (2018). A new frontier: the convergence of nanotechnology, brain-machine interfaces, and artificial intelligence. Frontiers in Neuroscience, 12.
Voeneky, S., et al. (2022). Towards a governance framework for brain data. Neuroethics, 15(2).
Kellmeyer, P. (2019). Artificial intelligence in basic and clinical neuroscience: opportunities and ethical challenges. Neuroforum, 25(4), 241-250.
Yuste, R., et al. (2017). Four ethical priorities for neurotechnologies and AI. Nature, 551(7679), 159-163.
Farisco, M., et al. (2022). On the contribution of neuroethics to the ethics and regulation of artificial intelligence. Neuroethics, 15(1).
Salles, A. (2024). Neuroethics and AI ethics: A proposal for collaboration. BMC Neuroscience, 25(1).
Sivanagaraju, D. (2024). Revolutionizing brain analysis: AI-powered insights for neuroscience. International Journal of Scientific Research in Engineering and Management, 08(12), 1-7.

Resilient AI: Advancing Robustness Against Adversarial Threats with D-ReLU

Artificial intelligence (AI) is now embedded in everyday life, from self-driving cars to medical diagnostic tools, enabling tasks to be performed faster and, in some cases, more accurately than humans. However, this rapid advancement comes with significant challenges, particularly in the form of adversarial attacks. These attacks exploit small, often imperceptible changes in input data to deceive AI systems into making incorrect decisions. For example, a strategically placed sticker on a stop sign might cause an AI-powered car to misinterpret it as a speed limit sign, creating potentially dangerous situations; another example can be small perturbations added to your dog’s picture, which can lead to state-of-the-art AI to confuse it with a cat:

The Role of ReLU and Its Limitations

The Rectified Linear Unit (ReLU) activation function is a foundational component of many AI models. Its simplicity and efficiency have made it a go-to choice for training deep learning networks. However, ReLU’s unrestricted output can make models vulnerable to adversarial noise, leading to cascading errors in predictions. Attempts to address this vulnerability, such as Static-Max-Value ReLU (S-ReLU or capped ReLU), have introduced fixed output caps, but these solutions often underperform on more complex datasets and tasks.

Introducing D-ReLU

D-ReLU represents a significant advancement over traditional ReLU. It incorporates a dynamic output cap that adjusts based on the data flowing through the network. This adaptability serves as a robust defense mechanism against adversarial inputs while maintaining computational efficiency. In essence, D-ReLU acts as a self-adjusting safeguard, preserving model integrity even under duress.

Key Features of D-ReLU:

Adaptive Output Limits: D-ReLU employs learnable caps that evolve during training, enabling models to balance robustness and accuracy effectively.
Enhanced Resilience: D-ReLU has demonstrated superior performance against adversarial attacks, including FGSM, PGD, and Carlini-Wagner, while maintaining consistent performance on standard datasets.
Scalability: Tested on large-scale datasets like CIFAR-10, CIFAR-100, and TinyImagenet, D-ReLU has proven its ability to scale effectively without degradation in performance.
Efficient Training: Unlike adversarial training methods, which require extensive additional computations, D-ReLU achieves robustness naturally, streamlining the training process.
Real-World Viability: D-ReLU excels in real-world scenarios, including black-box attack settings where attackers lack full knowledge of the model.

The Broader Implications

In applications where reliability and safety are paramount—such as autonomous vehicles, financial systems, and medical imaging—D-ReLU offers a compelling solution to the challenges posed by adversarial inputs. By enhancing a model’s resilience without sacrificing performance, D-ReLU provides a vital upgrade for AI systems operating in high-stakes environments.

Future Directions

The potential of D-ReLU extends beyond current implementations. Areas of exploration include:

Further optimization for improved performance,
Applications in natural language processing and audio tasks,
Integration with complementary robust training methods for enhanced results.

For a detailed analysis and technical insights, download our paper here. If you are working on AI models, we encourage you to experiment with D-ReLU and share your experiences:

Sooksatra, Korn, and Pablo Rivas. 2024. “Dynamic-Max-Value ReLU Functions for Adversarially Robust Machine Learning Models” Mathematics 12, no. 22: 3551. https://doi.org/10.3390/math12223551

About the Author

Korn Sooksatra is a Ph.D. student at Baylor University, specializing in adversarial machine learning and AI robustness.

Standard IEEE 7014

Sharing that IEEE 7014-2024: IEEE Standard for Ethical Considerations in Emulated Empathy in Autonomous and Intelligent Systems has been published!

This standard is the result of five years of dedication and collaboration by a diverse group of global experts, and Dr. Rivas has contributed at different stages. The journey was marked by passionate discussions, varied perspectives, and a unified goal of fostering ethical and responsible AI development.

As AI technology becomes increasingly powerful and integral to our daily lives, IEEE 7014-2024 represents a crucial step towards ensuring that these systems are developed with ethical considerations at the forefront.

Accessing the Standard

The full text of IEEE 7014-2024 can be viewed and purchased here: IEEE 7014. Additionally, free access may soon be available via the IEEE GET Program: IEEE GET Program, although this is currently to be confirmed.

Acknowledgments

A huge thank you to Ben Bland and all the wonderful people who contributed to this project. We worked together to reach a consensus and have made a significant contribution to the future of AI technology.

This publication is a testament to the power of collaboration and the shared vision of building a brighter technological future for humanity and our planet.

Final Thoughts

The publication of IEEE 7014-2024 is a proud moment for all who have been involved, including our very own Dr. Rivas. It underscores the importance of considering ethical implications in AI development and sets a precedent for future advancements in the field. We look forward to seeing how this standard will influence the development of AI systems that are not only intelligent but also empathetic and ethically sound.

Understanding the Executive Order on AI: Implications for the Industry and Academia

The White House recently released an executive order titled “Executive Order on the Safe, Secure, and Trustworthy Development and Use of Artificial Intelligence.” This directive aims to establish a framework for the responsible development and deployment of AI technologies in the United States. Here are a few key takeaways from this order and its implications for the AI industry and academic researchers.

1. What does this EO mean for the AI industry?

Regulatory Framework: The order emphasizes establishing a regulatory framework that ensures the safe and responsible development of AI. Companies must adhere to specific standards and best practices when developing and deploying AI technologies.
Transparency and Accountability: The industry is encouraged to adopt transparent methodologies and ensure that AI systems are explainable. This will likely lead to a surge in demand for tools and solutions that offer transparency in AI operations.
Collaboration with Federal Agencies: The order promotes cooperation between the private sector and federal agencies. This collaboration fosters innovation while ensuring AI technologies align with national interests and security.
Risk Management: Companies are urged to adopt risk management practices that identify and mitigate potential threats AI systems pose. This includes addressing biases, ensuring data privacy, and safeguarding against malicious uses of AI.

At the CRAIG/CSEAI, we’re committed to assisting industry and government partners in navigating this intricate AI regulatory terrain through our research, assessments, and training. Contact us to know more.

2. What does the EO mean for academics doing AI research?

Research Funding: The order highlights the importance of federal funding for AI research. Academics can expect increased support and resources for projects that align with the order’s objectives, especially those focusing on safety, security, and trustworthiness.
Ethical Considerations: Given the emphasis on trustworthy AI, researchers will be encouraged to incorporate ethical considerations into their work. This aligns with the growing movement towards AI ethics in the academic community.
Collaboration Opportunities: The directive promotes collaboration between academia and federal agencies. This could lead to new research opportunities, partnerships, and access to resources that were previously unavailable.
Publication and Transparency: The order underscores the importance of transparency in AI research. Academics will be encouraged to publish their findings, methodologies, and datasets to promote openness and reproducibility in the field.

The “Executive Order on the Safe, Secure, and Trustworthy Development and Use of Artificial Intelligence” is a significant step towards ensuring that AI technologies are developed and used responsibly. Both the AI industry and academic researchers have a pivotal role to play in realizing the order’s objectives. This order is, in part, a follow-up on prior white house’s effort to promote responsible AI.

AI Orthopraxy: Walking the Talk of Trustworthy AI

In today’s digital age, trust has become a precious commodity. It’s the invisible currency that fuels our interactions with technology and brands. Building trust, especially in technology, is a costly and time-consuming process. However, the payoff is immense. When users trust a system or a brand, they are more likely to engage with it, advocate for it, and remain loyal even when faced with alternatives.

One of the most effective ways to build trust in technology is to ensure it aligns with societal goals and values. When a system or technology operates in a way that benefits society and adheres to its values, it is more likely to be trusted and accepted.

However, artificial intelligence (AI) has faced significant challenges. Despite its immense potential and numerous benefits, trust in AI has suffered. This is due to various factors, including concerns about privacy, transparency, potential biases, and the lack of a clear ethical framework guiding its use.

This is where the concept of AI Orthopraxy comes in. AI Orthopraxy is all about the correct practice of AI. It’s about ensuring that AI is developed and used in a way that is ethical, responsible, and aligned with societal values. It’s about walking the talk of trustworthy AI.

In this talk, I will discuss the concept of AI Orthopraxy, the recent developments in AI, the associated risks, and the tools and strategies we can use to ensure the responsible use of AI. The goal is not just to highlight the challenges but also to provide a roadmap for moving forward in a way that is beneficial for all stakeholders.

Large Language Models (LLMs) and Large Multimodal Models: The Ethical Implications

The journey of Large Language Models (LLMs) has been remarkable. From the early successes of models like GPT and BERT, we have seen a rapid evolution in the capabilities of these models. The most recent iterations, such as ChatGPT, have demonstrated an impressive ability to generate human-like text, opening up many applications in areas like customer service, content creation, and more.

Parallel to this, the field of vision models has also seen significant advancements. Introducing models like Vision Transformer (ViT) has revolutionized how we process and understand visual data, leading to breakthroughs in medical imaging, autonomous driving, and more.

However, as with any powerful technology, these models come with their own challenges. One of the most concerning is their fragility, especially when faced with adversarial attacks. These attacks, which involve subtly modifying input data to mislead the model, have exposed the vulnerabilities of these models and raised questions about their reliability.

As someone deeply involved in this space, I see both the immense potential of these models and the serious risks they pose. But I firmly believe these risks can be mitigated with careful engineering and regulation.

Careful engineering involves developing robust models resistant to adversarial attacks and biases. It involves ensuring transparency in how these models work and making them interpretable so that their decisions can be understood and scrutinized.

On the other hand, regulation involves setting up rules and standards that guide the development and use of these models. It involves ensuring that these models are used responsibly and ethically and that there are mechanisms in place to hold those who misuse them accountable.

AI Ethics Standards: The Need for a Common Framework

Standards play a crucial role in ensuring technology’s responsible and ethical use. In the context of AI, they can help make systems fair, accountable, and transparent. They provide a common framework that guides the development and use of AI, ensuring that it aligns with societal values and goals.

One of the key initiatives in this space is the P70XX series of standards developed by the IEEE. These standards address various ethical considerations in system and software engineering and provide guidelines for embedding ethics into the design process.

Similarly, the International Organization for Standardization (ISO) has been working on standards related to AI. These standards cover various aspects of AI, including its terminology, trustworthiness, and use in specific sectors like healthcare and transportation.

The National Institute of Standards and Technology (NIST) has led efforts to develop a framework for AI standards in the United States. This framework aims to support the development and use of trustworthy AI systems and to promote innovation and public confidence in these systems.

The potential of these standards goes beyond just guiding the development and use of AI. There is a growing discussion about the possibility of these standards becoming recommended legal practice. This would mean that adherence to these standards would not just be a matter of ethical responsibility but also a legal requirement.

This possibility underscores the importance of these standards and their role in ensuring the responsible and ethical use of AI. However, standards alone are not enough. They need to be complemented by best practices in AI.

AI Best Practices: From Theory to Practice

As we navigate the complex landscape of AI ethics, best practices serve as our compass. They provide practical guidance on how to implement the principles of ethical AI in real-world systems.

One such best practice is the use of model cards for AI models. Model cards are like nutrition labels for AI models. They provide essential information about a model, including its purpose, performance, and potential biases. By providing this information, model cards help users understand what a model does, how well it does, and any limitations it might have.

Similarly, data sheets for datasets provide essential information about the datasets used to train AI models. They include details about the data collection process, the characteristics of the data, and any potential biases in the data. This helps users understand the strengths and weaknesses of the dataset and the models trained on it.

A newer practice is the use of Data Statements for Natural Language Processing, proposed to mitigate system bias and enable better science in NLP technologies. Data Statements are intended to address scientific and ethical issues arising from using data from specific populations in developing technology for other populations. They are designed to help alleviate exclusion and bias in language technology, lead to better precision in claims about how NLP research can generalize, and ultimately lead to language technology that respects its users’ preferred linguistic style and does not misrepresent them to others.

However, these best practices are only effective if a trained workforce understands them and can implement them in their work. This underscores the importance of education and training in AI ethics. It’s not enough to develop ethical AI systems; we must cultivate a workforce that can uphold these ethical standards in their work. Initiatives like the CSEAI promote responsible AI and develop a workforce equipped to navigate AI’s ethical challenges.

The Role of the CSEAI in Promoting Responsible AI

The Center for Standards and Ethics in AI (CSEAI) is pivotal in promoting responsible AI. Our mission at CSEAI is to provide applicable, actionable standard practices in trustworthy AI. We believe the path to responsible AI lies in the intersection of robust technical standards and ethical solid guidelines.

One of the critical areas of our work is developing these standards. We work closely with researchers, practitioners, and policymakers to develop standards that are technically sound and ethically grounded. These standards provide a common framework that guides the development and use of AI, ensuring that it aligns with societal values and goals.

In addition to developing standards, we also focus on state-of-the-art collaborative AI research and workforce development. We believe that responsible AI requires a workforce that is not just technically competent but also ethically aware. To this end, we offer training programs and resources that help individuals understand the ethical implications of AI, upcoming regulations, and the importance of bare minimum practices like Model Cards, Datasheets for Datasets, and Data Statements.

As the field of AI continues to evolve, so does the landscape of regulation, standardization, and best practices. At CSEAI, we are committed to staying ahead of these changes. We continuously update our value propositions and training programs to reflect the latest developments in the field and to ensure our standards and practices align with emerging regulations.

As the CSEAI initiative moves forward, we aim to ensure that AI is developed and used in a way that is beneficial for all stakeholders. We believe that with the right standards and practices, we can harness the power of AI in a way that is responsible, ethical, and aligned with societal values in a manner that is profitable for our industry partners and safe, robust, and trustworthy for all users.

Conclusion: The Future of Trustworthy AI

As we look toward the future of AI, we find ourselves amidst a cacophony of voices. As my colleagues put it, on one hand, we have the “AI Safety” group, which often stokes fear by highlighting existential risks from AI, potentially distracting from immediate concerns while simultaneously pushing for rapid AI development. On the other hand, we have the “AI Ethics” group, which tends to focus on the faults and dangers of AI at every turn, creating a brand of criticism hype and advocating for extreme caution in AI use.

However, most of us in the AI community operate in the quiet middle ground. We recognize the immense benefits that AI can bring to sectors like healthcare, education, and vision, among others. At the same time, we are acutely aware of the severe risks and harms that AI can pose. But we firmly believe that, like with electricity, cars, planes, and other transformative technologies, these risks can be minimized with careful engineering and regulation.

Consider the analogy of seatbelts in cars. Initially, many people resisted their use. We felt safe enough, with our mothers instinctively extending an arm in front of us during sudden stops. But when a serious accident occurred, the importance of seatbelts became painfully clear. AI regulation can be seen in a similar light. There may be resistance initially, but with proper safeguards in place, we can ensure that when something goes wrong—and it inevitably will—we will all be better prepared to handle it. More importantly, these safeguards will be able to protect those who are most vulnerable and unable to protect themselves.

As we continue to navigate the complex landscape of AI, let’s remember to stay grounded, to focus on the tangible and immediate impacts of our work, and to always strive for the responsible and ethical use of AI. Thank you.

This is a ChatGPT-generated summary of a noisy transcript of a keynote presented at Marist College on Tuesday, June 13, 2023, at 9 am as part of the Enterprise Computing Conference in Poughkeepsie, New York.

The White House Promotes Responsible AI: Here’s What It Means for the Industry

Today, we are on the brink of a new era where Artificial Intelligence (AI) promises to transform every aspect of our lives. However, with great power comes great responsibility. As AI permeates our societies and economies, ensuring its responsible use becomes more critical.

The Biden-Harris Administration has recently taken considerable steps to foster responsible AI innovation, protect citizens’ rights, and ensure safety. But what does this mean for industry players, particularly those who integrate AI into their products?

A Call for Responsibility

At the heart of the White House’s strategy is the principle that companies have a fundamental responsibility to ensure their products are safe before deployment. This safety-first approach means preventing harm and actively promoting the public good.

Meeting with CEOs of leading AI innovators, the Administration has underscored the importance of ethical and trustworthy AI systems, emphasizing safeguards to mitigate risks and potential harms.

Investing in Responsible AI

The Biden-Harris Administration is backing up its words with actions, committing $140 million to launch seven new National AI Research Institutes. These will bring the total number of institutes to 25 nationwide, and each is committed to ethical, responsible AI that serves the public good.

The Role of the NSF IUCRC, Center for Standards and Ethics in AI (CSEAI)

This is where our initiative, the NSF IUCRC, Center for Standards and Ethics in AI (CSEAI), comes into play. We align perfectly with the Administration’s vision for responsible AI, focusing on establishing standards and ethics that serve as the bedrock for AI development and application.

By joining and funding the CSEAI, industry members will directly collaborate with other industry members and with academia, contributing to responsible AI research and advancement. This aligns with the White House’s call for ethical and safe AI and benefits companies in the long run, ensuring their products meet the highest ethical and safety standards.

What this Means for AI Developers and Users

The White House’s recent announcements signal a shift towards more stringent AI development and use standards. This means industries must prioritize building and deploying AI systems that are ethical, trustworthy, and serve the public good.

In a world where AI is becoming ubiquitous, failing to meet these standards can lead to reputational damage, regulatory penalties, and even legal liability. Conversely, those who embrace these principles stand to gain significant competitive advantage, building trust with users and staying ahead of the regulatory curve.

Conclusion

The White House’s commitment to responsible AI is not just good news for Americans—it’s a call to action for industry members who develop or use AI. By aligning with the principles of responsible AI and supporting initiatives like the NSF IUCRC, Center for Standards and Ethics in AI (CSEAI), industry players can meet their ethical obligations and secure their future place in AI.

Join us in making AI safe, ethical, and beneficial for all.

(Editorial) Designing AI Using a Human-Centered Approach: Explainability and Accuracy Toward Trustworthiness

In the rapidly evolving world of artificial intelligence (AI), the IEEE Transactions on Technology and Society recently published a special issue that delves into the heart of AI’s most pressing challenges and opportunities. This editorial piece has garnered widespread attention. Read the full editorial here.

J. R. Schoenherr, R. Abbas, K. Michael, P. Rivas and T. D. Anderson, “Designing AI Using a Human-Centered Approach: Explainability and Accuracy Toward Trustworthiness,” in IEEE Transactions on Technology and Society, vol. 4, no. 1, pp. 9-23, March 2023, doi: 10.1109/TTS.2023.3257627.

The Essence of the Special Issue

This special issue comprises eight thought-provoking papers that collectively address the multifaceted nature of AI. The journey begins with a reconceptualization of AI, leading to discussions on the pivotal role of explainability and accuracy in AI systems. The papers emphasize that designing AI with a human-centered approach while recognizing the importance of ethics is not a zero-sum game.

Key Highlights

Reconceptualizing AI: Clarke, a Fellow of the Australian Computer Society, revisits the original conception of AI and proposes a fresh perspective, emphasizing the synergy between human and artifact capabilities.
The Challenge of Explainability: Adamson, a Past President of the IEEE’s Society on the Social Implications, delves into the complexities of AI systems, highlighting the concealed nature of many AI algorithms and the need for post-hoc reasoning.
Trustworthy AI: Petkovic underscores that trustworthy AI requires both accuracy and explainability. He emphasizes the importance of explainable AI (XAI) in ensuring user trust, especially in high-stakes applications.
Bias in AI: A team of researchers, including Nagpal, Singh, Singh, Vatsa, and Ratha, evaluates the behavior of face recognition models, shedding light on potential biases related to age and ethnicity.
AI in Healthcare: Dhar, Siuly, Borra, and Sherratt discuss the challenges and opportunities of deep learning in the healthcare domain, emphasizing the ethical considerations surrounding medical data.
AI in Education: Tham and Verhulsdonck introduce the “stack” analogy for designing ubiquitous learning, emphasizing the importance of a human-centered approach in smart city contexts.
Ethics in Computer Science Education: Peterson, Ferreira, and Vardi discuss the role of ethics in computer science education, emphasizing the need for emotional engagement to understand the potential impacts of technology.

A Call to Action

As guest editors deeply engaged in human-centric approaches to AI, we challenge all stakeholders in the AI design process to consider the multidimensionality of AI. It’s crucial to move beyond the trade-offs mindset and prioritize accuracy and explainability. If a decision made by an AI system cannot be explained, especially in critical sectors like finance and healthcare, should it even be proposed?

This special issue is a testament to the importance of ethics, accuracy, explainability, and trustworthiness in AI. It underscores the need for a human-centered approach to designing AI systems that benefit society. For a deeper understanding of each paper and to explore the insights shared by the authors, check out the full special issue in IEEE Transactions on Technology and Society.

How to Show that Your Model is Better: A Basic Guide to Statistical Hypothesis Testing

Do you need help determining which machine learning model is superior? This post presents a step-by-step guide using basic statistical techniques and a real case study! 🤖📈 #AIOrthoPraxy #MachineLearning #Statistics #DataScience

When employing Machine Learning to address problems, our choice of a model plays a crucial role. Evaluating models can be straightforward when performance disparities are substantial, for example, when comparing two large-language models (LLMS) on a masked language modeling (MLM) task with 71.01 and 28.56 perplexity, respectively. However, if differences among models are minute, making a solid analysis to discern if one model is genuinely superior to others can prove challenging.

This tutorial aims to present a step-by-step guide to determine if one model is superior to another. Our approach relies on basic statistical techniques and real datasets. Our study compares four models on six datasets using one metric, standard accuracy. Alternatively, other contexts may use different numbers of models, metrics, or datasets. We will work with the tables below that show the properties of the datasets and the performance of two baseline models and two of our proposed models, for which we hope to show that they are better, which would be our hypothesis to be tested.

Summary of performance measured with standard accuracy

Summary of the main properties of the datasets considered in this tutorial.

One of the primary purposes of statistics is hypothesis testing. Statistical inference involves taking a sample from a population and determining how well the sample represents the population. In hypothesis testing, we formulate a null hypothesis, $H_0$ , and an alternative hypothesis, $H_A$ , based on the problem (comparing models). Both hypotheses must be concise, mutually exclusive, and exhaustive. For example, we could say that our null hypothesis is that the models perform equally, and the alternative could mean that the models perform differently.

Why is the ANOVA test not a good alternative?

The ANOVA (Analysis of Variance) test is a parametric test that compares the means of multiple groups. In our case, we have four models to compare with six datasets. The null hypothesis for ANOVA is that all the means are equal, and the alternative hypothesis is that at least one of the means is different. If the $p-$ value of the ANOVA test is less than the significance level (usually 0.05), we reject the null hypothesis and conclude that at least one of the means is different, i.e., at least one model performs differently than the others. However, ANOVA may not always be the best choice for comparing the performance of different models.

One reason for this is that ANOVA assumes that the data follows a normal distribution, which may not always be the case for real-world data. Additionally, ANOVA does not take into account the difficulty of classifying certain data points. For example, in a dataset with a single numerical feature and binary labels, all models may achieve 100% accuracy on the training data. However, if the test set contains some mislabeled points, the models may perform differently. In this scenario, ANOVA would not be appropriate because it does not account for the difficulty of classifying certain data points.

Another issue with ANOVA is that it assumes that the variances of the groups being compared are equal. This assumption may not hold for datasets with different levels of noise or variability. In such cases, alternative statistical tests like the Friedman test or the Nemenyi test may be more appropriate.

Friedman test

The Friedman test is a non-parametric test that compares multiple models. In our example, we want to compare the performance of $k=4$ different models, i.e., two baseline models, Gabor randomized, and Gabor repeated, on $N=6$ datasets. First, the test calculates the average rank of each model’s performance on each dataset, with the best-performing model receiving a rank of 1. The Friedman test then tests the null hypothesis, $H_0$ , that all models are equally effective and their average ranks should be equal. 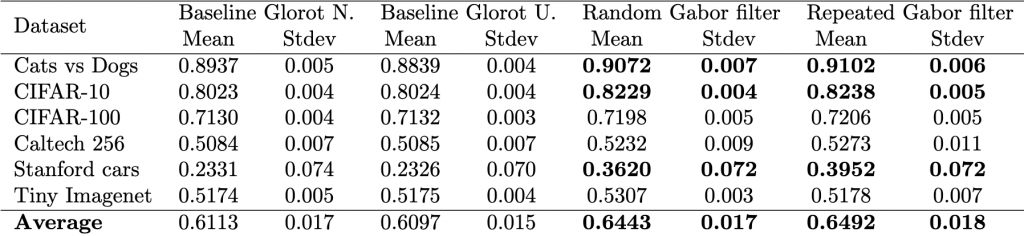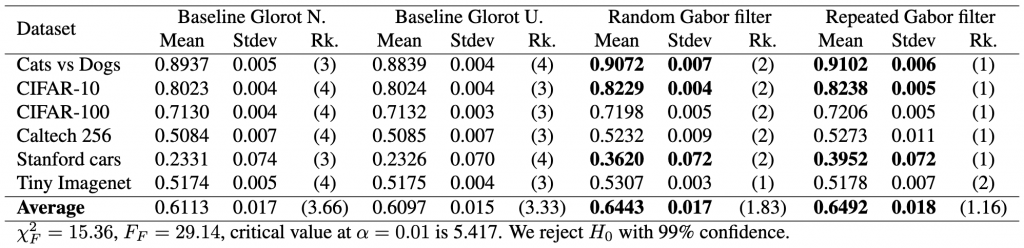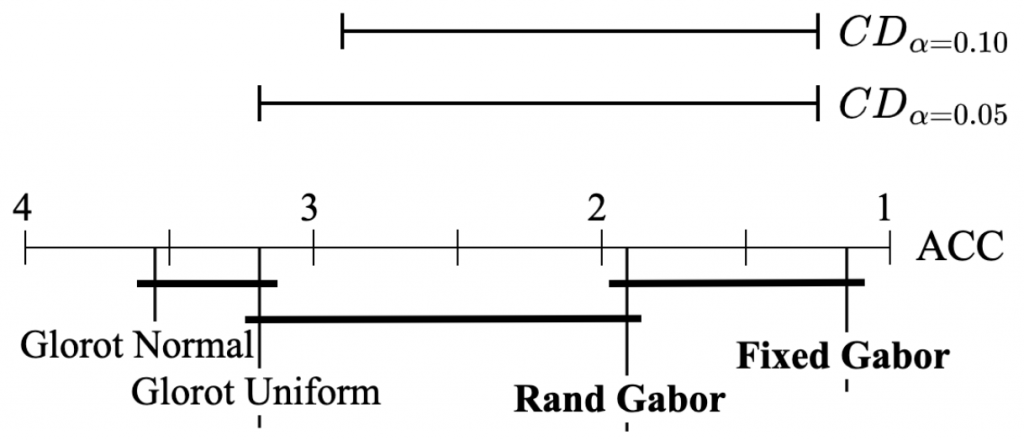The test statistic is calculated as follows:

(1) $\begin{equation*} \chi_{F}^{2}=\frac{12 N}{k(k+1)}\left[\sum_{j=1}^{k} R_{j}^{2}-\frac{k(k+1)^{2}}{4}\right] \end{equation*}$

where $R$ is the average ranking of each model.

The test result can be used to determine whether there is a statistically significant difference between the performance of the models by making sure that $\chi_{F}^{2}$ is not less than the critical value for the $F$ distribution for a particular confidence value $\alpha$ . However, since $\chi_{F}^{2}$ could be too conservative, we also calculate the $F_F$ statistic as follows:

(2) $\begin{equation*} F_{F}=\frac{(N-1) \chi_{F}^{2}}{N(k-1)-\chi_{F}^{2}}. \end{equation*}$

Based on the critical value, $F_{F}$ , and $\chi_{F}^{2}$ , we evaluate $H_0$ ; once the null hypothesis is rejected, we apply a posthoc test. For this, we use the Nemenyi test to establish whether models differ significantly in their performance.

We will start the process of getting this test done by ranking the data. First, we can load the data and verify it with respect to the table shown earlier.

import pandas as pd
import numpy as np

data = [[0.8937, 0.8839, 0.9072, 0.9102],
        [0.8023, 0.8024, 0.8229, 0.8238],
        [0.7130, 0.7132, 0.7198, 0.7206],
        [0.5084, 0.5085, 0.5232, 0.5273],
        [0.2331, 0.2326, 0.3620, 0.3952],
        [0.5174, 0.5175, 0.5307, 0.5178]]

model_names = ['Glorot N.', 'Glorot U.', 'Random G.', 'Repeated G.']

df = pd.DataFrame(data, columns=model_names)

print(df.describe())  #<- use averages to verify if matches table

Output:

       Glorot N.  Glorot U.  Random G.  Repeated G.
count   6.000000   6.000000   6.000000     6.000000
mean    0.611317   0.609683   0.644300     0.649150
std     0.240422   0.238318   0.206871     0.200173
min     0.233100   0.232600   0.362000     0.395200
25%     0.510650   0.510750   0.525075     0.520175
50%     0.615200   0.615350   0.625250     0.623950
75%     0.779975   0.780100   0.797125     0.798000
max     0.893700   0.883900   0.907200     0.910200

Next, we rank the models and get their averages like so:

data = df.rank(1, method='average', ascending=False)
print(data)
print(data.describe())

Output:

   Glorot N.  Glorot U.  Random G.  Repeated G.
0        3.0        4.0        2.0          1.0
1        4.0        3.0        2.0          1.0
2        4.0        3.0        2.0          1.0
3        4.0        3.0        2.0          1.0
4        3.0        4.0        2.0          1.0
5        4.0        3.0        1.0          2.0

       Glorot N.  Glorot U.  Random G.  Repeated G.
count   6.000000   6.000000   6.000000     6.000000
mean    3.666667   3.333333   1.833333     1.166667
std     0.516398   0.516398   0.408248     0.408248
min     3.000000   3.000000   1.000000     1.000000
25%     3.250000   3.000000   2.000000     1.000000
50%     4.000000   3.000000   2.000000     1.000000
75%     4.000000   3.750000   2.000000     1.000000
max     4.000000   4.000000   2.000000     2.000000

With this information, we can expand our initial results table to show the rankings by dataset and the average rankings across all datasets for each model.

Now that we have the rankings, we can proceed with the statistical analysis and do the following:

(3) $\begin{align*} \chi_{F}^{2}&=\frac{12 \cdot 6}{4 \cdot 5}\left[\left(3.66^2+3.33^2+1.83^2+1.16^2\right)-\frac{4 \cdot 5^2}{4}\right] \nonumber \\ &=15.364 \nonumber \end{align*}$

(4) $\begin{equation*} F_{F}=\frac{5 \cdot 15.364}{6 \cdot 3-15.364}=29.143 \nonumber \end{equation*}$

The critical value at $\alpha=0.01$ is 5.417. Thus, because the critical value is below our statistics obtained, we reject $H_0$ with 99% confidence.

The critical value can be obtained from any table that has the F distribution. In the table the degrees of freedom across columns (denoted as $df_1$ ) is $k-1$ , that is the number of models minus one; the degrees of freedom across rows (denoted as $df_2$ ) is $(k-1)\times(N-1)$ , that is, the number of models minus one, times the number of datasets minus one. In our case this is $df_1=3$ and $df_2=15$ .

Nemenyi Test

The Nemenyi test is a post-hoc test that compares multiple models after a significant result from Friedman’s test. The null hypothesis for Nemenyi is that there is no difference between any two models, and the alternative hypothesis is that at least one pair of models is different.

The formula for Nemenyi is as follows:

$CD = q_{\alpha} \sqrt{\frac{k(k+1)}{6N}}$

where $q_{\alpha}$ is the critical difference of the Studentized range distribution at the chosen significance level and $k$ is the number of groups. The $q_{\alpha}$ value can be obtained from the following table:

Critical values for the Nemenyi test, which is conducted following the Friedman test, with two-tailed results.

Thus, for our particular case study, the critical differences are:

(5) $\begin{equation*} CD_{\alpha=0.05}=2.569 \sqrt{\frac{4 \cdot 5}{6 \cdot 6}} = 1.915 \nonumber \end{equation*}$

(6) $\begin{equation*} CD_{\alpha=0.10}=2.291 \sqrt{\frac{4 \cdot 5}{6 \cdot 6}} = 1.708 \nonumber \end{equation*}$

Since the difference in rank between the randomized Gabor and baseline Glorot normal is 1.83 and is less than the $CD_{\alpha=0.10}=1.708$ , we conclude Gabor is better. Similarly, since the difference in rank between the fixed Gabor and baseline Glorot uniform is 2.17 and is less than the $CD_{\alpha=0.05}=1.915$ , we conclude that Gabor is better. Yes, there is sufficient statistical evidence to show that our model is better with high confidence.

Things we would like to see in papers

First of all, it would be nice to have a complete table that includes the results of the statistical tests as part of the caption or as a footnote, like this:

Second of all, graphics always help! A simple and visually appealing diagram is a powerful way to represent post hoc test results when comparing multiple classifiers. The figure below, which illustrates the data analysis from the table above, displays the average ranks of methods along the top line of the diagram. To facilitate interpretation, the axis is oriented so that the best ranks appear on the right side, which enables us to perceive the methods on the right as superior.

Comparison of all models against each other with the Nemenyi test. Models not significantly different at α = 0.10 or α = 0.05 are connected.

When comparing all the algorithms against each other, the groups of algorithms that are not significantly different are connected with a bold solid line. Such an approach clearly highlights the most effective models while also providing a robust analysis of the differences between models. Additionally, the critical difference is shown above the graph, further enhancing the visualization of the analysis results. Overall, this simple yet powerful diagrammatic approach provides a clear and concise representation of the performance of multiple classifiers, enabling more informed decision-making in selecting the best-performing model.

Main Sources

The statistical tests are based on this paper:

Demšar, Janez. “Statistical comparisons of classifiers over multiple data sets.” The Journal of Machine learning research 7 (2006): 1-30.

The case study is based on the following research:

Rai, Mehang. “On the Performance of Convolutional Neural Networks Initialized with Gabor Filters.” Thesis, Baylor University, 2021.

President’s Executive Order for Advancing Racial Equity in AI Systems: What It Means for the Future of AI-Based Technology

Summary: The President of the United States, Joe Biden, has recently authorized an Executive Order intending to enhance racial equity and foster support for marginalized communities via the federal government. The Order mandates that federal agencies employing artificial intelligence (AI) systems assume novel equity responsibilities and instructs them to forestall and rectify any form of discrimination, including safeguarding the public from the perils of algorithmic discrimination.

What you should know: The recent Executive Order on Further Advancing Racial Equity and Support for Underserved Communities Through The Federal Government emphasizes the importance of advancing equity for all, including communities that have long been underserved, and addressing systemic racism in the US policies and programs. This order implies that AI systems should be designed to ensure that they do not perpetuate or exacerbate inequities and should be used to address the unfair disparities faced by underserved communities. It is also implied that the Federal Government should work with civil society, the private sector, and State and local governments to redress unfair disparities and remove barriers to Government programs and services, which could be facilitated by the development and deployment of ethical and responsible AI systems. Additionally, the order emphasizes the need for evidence-based approaches to equitable policymaking and implementation, which can be achieved through collecting and analyzing data on the impacts of AI systems on different communities. Therefore, AI practitioners should ensure that their systems are designed, developed, and deployed to promote equity, fairness, and inclusivity and are aligned with the Federal Government’s commitment to advancing racial equity and supporting underserved communities.

The Center for Standards and Ethics in Artificial Intelligence (CSEAI)

Following President’s Executive Order, we at the CSEAI recognize the critical role of artificial intelligence in promoting fairness, accountability, and transparency. As a research center committed to developing responsible AI techniques, we believe our work can help meet the challenges and opportunities of emerging regulation, standardization, and best practices in AI systems. We are inviting industry members to partner with us financially and take part in collaborative research on trustworthy AI. Our mission is to provide applicable, actionable, standard practices in trustworthy AI and train a workforce that enables fairness, accountability, and transparency. We believe our work will help mitigate AI adoption’s operational, liability, and reputation risks.

The CSEAI brings together leading universities to conduct collaborative research in responsible AI techniques. We are committed to workforce development and providing accessible standards, best practices, testing, and compliance. We are proud to be a part of the NSF IUCRC Program and are excited to be supported by the NSF, which provides a standard agreement, organizational, and legal framework.

Join us in creating a better future for all Americans by developing responsible AI practices that promote fairness, accountability, and transparency. By partnering with the CSEAI, you will have the opportunity to work with a dedicated team of researchers, participate in cutting-edge research, and help shape the future of AI. Contact us today to learn more about partnering with the CSEAI.

Contact Pablo_Rivas@Baylor.edu and find out more at www.cseai.center.

(Editorial) Emerging Technologies, Evolving Threats: Next-Generation Security Challenges

The Volume 3, Issue 3, of the IEEE Transactions on Technology and Society is officially published with great contributions regarding security challenges posed by emerging technologies and their effects on society.

Our editorial piece is freely accessible and briefly introduces the research on this issue and how relevant these issues are. Our discussion briefly discusses GPT and DALEE, as means to show the great advances of AI and some ethical considerations around those. Take a look:

T. Bonaci, K. Michael, P. Rivas, L. J. Robertson and M. Zimmer, “Emerging Technologies, Evolving Threats: Next-Generation Security Challenges,” in IEEE Transactions on Technology and Society, vol. 3, no. 3, pp. 155-162, Sept. 2022, doi: 10.1109/TTS.2022.3202323.